|
高级桥牌战术
[英]特伦斯·里斯 著 钱尚武
、孙怀民、朱允伦 译
|
.
返回目录
|
第一章 算 牌
优秀桥手和普通桥手的主要区别在于：优秀桥手能估计到全部五十二张牌，而普通桥手只是根据他所看到的二十六张牌来打牌。即使一个桥手可能懂得很多高级战术，但是如果他盲目地打牌，而不去估算对方手中的牌，那么他也不能打出中等以上的水平。如果一个桥手能经常估算对方手中的牌，那么，即使他对坚壁清野法懂得很少，甚至完全不了解紧逼法，他也仍然是一个千里挑一的好桥手。
估计对方的牌，并不需要特殊的天才，比如，从防御方面来说，首攻花色的牌型分布，往往在第一轮就能大致确定下来，第二轮则几乎成为定局了。而当定约者吊了一两轮将牌后，就能有百分之九十的把握说出定约者本来有几张将牌。所以，在大多数场合下，打了三四轮就知道两种花色的分布，于是再经过一两轮的出牌就能作出对整个牌型的估计。这种分析并没有什么十分困难和神秘的地方，但却需要经常不断的努力，而这只有很少桥手能作到这一点。
对定约者说，猜防御方的牌张分布要比较困难一些，特别是在缺乏叫牌信息时，它的根据就更少了。在打牌初期，定约者往往只能根据几率和对称理论去猜牌；随着牌局的继续进行，对手的牌型会越来越清楚。下面的一手牌，虽然没有很令人注目的地方，但是用它作为讨论的起点是很有启发的。
东西有局。北开叫；叫牌过程如下：
|
北
|
东
|
南
|
西
|
|
1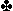
|
1
|
2
|
3
|
|
4
|
4
|
5
|
—
|
|
—
|
=
|
|
西家首攻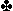A，然后又出第二张黑桃，南家将吃。现在的问题是要正确判断几个Q的位置。定约者认为既然敌方在有局时能叫到4，则将牌3-1分布比2-2分布的可能性更大些，所以吊第二轮将牌而东有将牌跟进时就用J飞。
此关一过，还要判断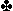Q的位置。既然西家持单张红心，他持草花长套可能性就大，为了完成牌型的估计，南家在出草花之前，先出了三轮方块，这样就确定了东家有六张红牌。既然东家曾争叫1，他很可能有六张黑桃，所以南家很有信心地飞了西家的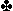Q，结果只丢给A和
A两墩牌，完成了定约。
大多数桥手能打成这副牌，尽管这副牌不难打，却提出了几个重要问题。首先，对于东西方牌型分布情况知道得很少时，就飞将牌，这是因为根据叫牌信息，猜到了将牌的3-1分布比2-2分布的可能性大。但是如果对方没有叫过牌，那么是飞张好还是击落好呢？答案要靠两种依据而定，一是简单的几率，二是对称理论；几率是比较可靠的根据，所以先来看这方面。
简单几率
几张牌在外时，其分布的几率列举如下：
两张牌在外，1-1分布52%，2-0分布48%。因此假设其他条件相同，外面两张牌中有一张为K时，击落打法比飞张打法稍好些。
三张牌在外，2-1分布78%，3-0分布22%。
四张牌在外，3-1分布50%，2-2分布40%，4-0分布10%。虽然3-1分布的几率大于2-2分布的几率，但不能由此得出结论，有九张牌缺一张Q时，飞张打法比击落打法为好。因为每出一张牌，几率估计都要发生变化。当定约者到了要打这花色的第二张牌时，击落比飞张的几率稍大些。所以在前面所讲的一手牌中，打第二轮将牌时，根据简单的几率，击落打法要比飞张打法有利。
五张牌在外，3-2分布68%，4-1分布28%，5-0分布4%。
六张牌在外，4-2分布48%，3-3分布36%，5-1分布15%，6-0分布1%。
七张牌在外，4-3分布62%，5-2分布31%，6-1分布7%，7-0分布小于0.5%。
几率的知识，对打牌是相当重要的。例如，定约者应该知道，成败机会根占一半的飞张，要比六张牌在外时牌张按3-3分布的几率大，但比起七张牌在外时牌张按4-3分布的几率却要小。当然还要考虑其他因素，比如说，由叫牌过程或出牌过程可知对方之一有个特长套，这时他的同伴就可能有另一花色的特长套。除这种直接的推断外，还有另一种因素需要考虑，即所谓对称理论。
对称理论
有些桥手将这称为对称定律，但这至多只是一种理论，其主要内容是：桥手可根据自己手里牌型推算他人的牌型以及四种花色的分布状况。一桥手手里有四张套，他可以根据对称理论估算出这种花色其余九张牌的分布情形。信仰对称理论的人认为牌张分布的几率要受到桥手手中牌型的影响。如桥手所持的牌是普通的4-4-3-2牌型，则他们会说，四张套其余九张牌也会具有类似的平均分布；如手中牌型是7-4-1-1，则四张套其余九张牌的分布也会有类似的不平均分布，诸如5-4-3-2，6-4-2-1，甚至于7-4-1-1。
简单说来，对称理论告诉我们，如你手中所持为不平均牌型，例如6-5-1-1，则对你所持长套牌说，其余在外牌的分布也会是很不平均的。
这里必须立刻声明，这种论断并没有得到数学家的支持。很容易证明，把一副牌分成两个26张牌组，一个26张牌组的分布不会影响另外一个26张牌组的分布。虽然如此，但这种合理的论断可能将事情过分简单化了。牌洗得不彻底的事实使数学几率不能代表实际打牌时真实的可能性。大多数专家桥手的意见是，不平均牌型在同一手牌中有共存的倾向。当明手或它们自己手中的牌型不平均时，他们宁肯按3-1分布打牌，而不愿按2-2分布打牌。在能够判断的范围内，经验会支持这种信念，即一个单张似会为另一个单张所平衡。开头所讲的那手牌就是一个例子，一个坚信对称理论的人，由于手中持有6-4-2-1这种不平均牌型，在处理将牌时就会去飞牌而不去击落将牌。
有一个更过火的信念，就是认为对自己所持长套来说，其余在外的牌的分布情况酷似手中的牌型。如所持牌型为7-2-2-2，则七张套的其他六张的分布也是2-2-2。
结论是，有两个机会从数学上看几率很相近时，则有对称理论作指引，总比没有好一些。例如，有九张牌缺Q时，如有一门花色有一单张，则按3-1分布打比较好些。
避免飞牌的算度
在我们开头的一手牌中还有一个值得注意之点：即定约者打了三轮方块，从而估计出敌方牌型。虽然一般说来定约者的估算要比防御者困难，但定约者有这样一个优越条件，就是他可以制定一个出牌计划来了解牌型，下面一手牌就是个例子：
在西家争叫1后，由南家主打4。西家首攻K，一连出了三轮黑桃，意图是消灭明手的9。南家出红心，西家在第二轮时拿进，回一张红心。现在定约者要设法避免草花失墩。有方块3-3分布的希望，还有飞草花的机会。在试探方块之前，正确的打法是：南家打出最后一张将牌，明手垫一张草花，然后连打三轮方块，发现东家还有一张方块，于是就出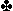K，然后又出一张草花，东家跟10。但是由于南家知道东家还有一张方块，所以决定不飞草花，结果，果然击落了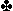Q，这样做并不是由于考虑到西家的牌而是由于算出了东家的牌。
探查牌型
上面这个例子，生动地说明了一个优秀选手和一个普通选手的区别；前者利用一切可能的机会去弄清牌型分布，而后者的打牌却根本不去考虑别人手里的牌。下面是一个运用同一原则但更高深一些的例子：
西家争叫1后，南家主打5。事实上这手牌打3NT较容易。西家首攻K，东出2。西家改出方块，定约者连吊两轮将牌，停在明手。这是有道理的。南家看到他可能还要丢一墩黑桃和一墩草花。他希望弄清黑桃的分布，因此就要弄清草花的分布，必要时又可以打四轮草花来弄清这一点。南家出草花时，希望由西家拿墩，因为如果让东家出牌回攻红心而被迫将吃的话，计划要受到干扰，所以南家在第四轮由明手出了一张小草花，自己手中出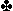J，让西家用K拿进。西家回了一张草花，明手拿进。由明手再出一轮草花，南家将吃，吊出最后一张将牌，打出一张小黑桃，用明手10飞成；然后由明手出第四轮草花将吃时，弄清西家手中有四张草花。既然前已弄清西家有两张方块，而因西家曾争叫过红心，他手中很可能持有五张红心牌张。由此可以得出结论，西家手中只剩K一张，于是南家出小黑桃（而不是大牌），给明手的A拿。假设西家只有三张草花，那南家就会认为他有三张黑桃，因而是3-5-2-3牌型。我们当还记得，东家在第一轮出的是2，这说明东家有三张红心，而不是两张红心。
推理和假设
下面一手牌比前面一些例子显得更难一些。定约者的思考过程向纵身发展，他据以估算敌方牌型的前提完全是假想的。
南家（第三家）开叫1，西家争叫2，北家加叫2，东家叫4，南家叫4。
西家首攻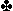3，东家用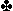A拿进，回一张2，西家用J拿进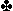，出K，再出A。在实际打牌时，南家用2将吃，再出Q。结果，虽然方块的分布合乎理想，但他还是宕了一墩，因还得丢一墩将牌。虽然没有理由去假设西家是单张K，但南家只应根据这种假设去打才能完成定约。
推理如下：对方的草花是4-4分，红心是5-4分；定约者不能在方块上丢一墩，他必须假设东家的方块是KX，则西家是XXX。果真如此，西家只能有一张黑桃，而唯一希望是西家有单张K。
算出牌张的位置
有时从出牌过程推算，可以十分精确地确定牌的位置，例如下面一手牌，定约者打得十分成功。
东西方已有40分（双局桥牌），西家开叫2（用的是两草花系统），北家、东家不叫，南家叫2，西家加倍。因西家开叫二，加倍是惩罚性的而不是技术性的。明手放下牌后，南家就感到叫牌过于冒失，处境十分困难，因为叫牌过程表明东家只有单张红心。西家出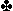K，东家打出不欢迎信号，西家转出一张小黑桃由明手10拿墩，定约者再回送一墩黑桃给西家。在这过程中东家本应该在垫牌时打出将牌先大后小信号，表示他有第三张将牌可以将吃红心，然而东家大意而没有这样做，这使西家感到很为难，经过长时间的考虑之后，他出了张小红心，因为他不希望丢掉红心的控制权。南方用明手的K拿进，并抛出自己手中的10，然后从明手出一张方块，南家在出这张牌前考虑了一下，他估计西家的牌，红心没有问题是五张，黑桃是四张，草花是三张而方块是单张。既然他没有出方块来解围，说明他很可能是单张K，所以南家用A击落K，然后出Q，9。这时如果西家放过这张红心，他仍能击败定约。不过他这时有点糊涂，而用A拿进，出掉手中将牌大牌，然后又出红心。南家用8飞成，再把草花垫在Q上，然后由明手出小方块而用10飞，结果完成了一个毫无希望的定约。
从牌的打法来推算
我们很容易指出上一手牌中西家的防御错误，虽然事实上在出牌时他是有困难的。这手牌的价值在于定约者当从明手出方块时推算出西家有单张K。作出这种推算正是第一流选手的标志。在打每一手牌时都有很多推算，但除了最明显的以外，其他的都为大多数桥手所忽略了。当定约者动某一花色时，防御方即能由此作出某种推算；同样地，定约者不动某种花色时，也必有某种缘故，防御方也能由此作出某种推算。
当定约者不动某一套时
打无将定约时，定约方不去动明手的某一个好套（如AQJX或AQJXX），你作为防御方，能作出什么推想呢？经常发生的是，防御者在得到赢墩后，会去进攻这个套，以为定约者不动这个套，就好象他没有K。这理由是很浅薄的。如他没有K，他多半在牌局的初期就要设法去树立这个套。当定约者不动这个套时，多半他手里有这个套的K，而是设法在旁处寻找第九个赢墩。同样，如果明手持有一个KQ带头的套（如KQ10X或KQXXX），而定约者不动这个套时，他多半持有这个套的A。
当明手持有QJXXX的套而定约者不去动它时，他多半没有K，也不大可能持有AX或AXX，他可能有单张A，或者是单张小牌。如果他的张数多，多半要动这个套。
当定约者不去动KJXXX或AJXXX套时，就特别值得注意，定约者有Q的可能性很小。如果他持有这个花色两张或三张小牌，他很可能会动这个套。因此，最可能的是，他持有这个套的AX或KX，他正在弄清其他套的情况，以便决定在这个套中到底要拿几墩。
如果定约者不去动AJ10X或AJ10XX套时，多半可以肯定他持有K甚至KQ。对其他各种组合也可作类似的推论。读者可以自行研究，这时一种很好的练习。
当定约者动某一套时
当定约者动某一套时，防御者可有正反两方面的推理。比如打无将定约，定约者首先打的花色往往是强套，防御者不应过早地放弃对此套的控制。当防御者持A时，而此A在明手的KQ之后，他往往还能忍让一轮而保住控制权。但是，如果定约者从明手出XXX套的牌，并且手上打出K时，他左方的防御者却很少不用A拿进，这就会过早地放弃对此套的控制权，因为这时定约者不可能没有其他的大牌。如定约者能让防御者较早地放弃控制，就会使很多牌好打得多。下面是一典型的例子：
西首攻J
定约是3NT。西家首攻J，南家拿进。看起来，定约毫无问题，因为这手牌没有明显的弱点。但当定约者连续用K，K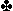，Q拿墩之后，他就感到没有把握了。当然，他若打对花色，定约完成不难。然而由于防御者没有过早地显示牌张的位置，就使得南家打牌困难得多了。
当对方动一个套时，所能作出的推论是多种多样的。在所有关键性的情形下，即必须在两种打法种选择一种时，桥手就应该自问，他所采取的观点是否与已知的事实相符。下面的残局是个很好的例子：
将牌是红心，要由西家出牌。西家出一张小黑桃，明手出小牌，东家出K，南家用A拿进，打回一张黑桃，明手出J，结果他在黑桃上就丢失两墩。如果他思路正确，就不会在第二轮猜错了。事实上，只有在东家持有K10X时，定约者出J才能拿墩。如果这样，则东家第一轮就会用10去飞，而不会出K了。下面所示黑桃的分布情况，可以作为上述例子的补充说明：
|
|
J 8 X
|
|
Q 10 X X
|
|
K X X
|
|
|
A 9 X
|
如要由西家出这个套，则他出小黑桃时，定约者不会感到困难。因此，他最好打出Q。南家用A拿进，出一张小牌，西家跟出小牌。试问这时南家应该让明手出哪一张牌呢？答案是：如果西家持有KQX，那么，他的正常打法是，第一张牌出小牌，而不是出K或Q。因此，除了对付一个特别机智的防御者这种情形以外，南就应该用8飞。
战术推理
每手牌防御方都可根据定约者的战术，作出某种推理。在有将定约中，定约者如何出将牌是值得注意的。假如定约者不准备用明手将牌吃张而吊将牌，就可断定明手的某个短套在定约者手中是没有失张的，也很可能他的这一套也是短套。如果防御者不作这种特殊推理，往往会中对方假紧逼之计。
当明手有一长套副牌，而定约者不去树立时，可以作出两种推理：一是他的将牌不够强，不足以用将吃方法来树立这个套；另一是他手中的这个花色很弱，从而使他感到没有树立的希望。
当定约者不吊将牌时，也可以作出某种推理，他或者是想用明手将牌将吃，或者准备交叉将吃。
在打无将定约时，防御者应该经常研究定约者的主攻方向。上面曾指出，当定约者不去动明手的一个好套时，往往是因为这个套是坚固套，而他需要在其他花色寻找所欠缺的赢墩。同样，如果定约者不动他自己曾叫得很凶的花色，这也很可能是由于这个套足够坚强，他也必须留心受骗，很可能定约者动的是他最弱的套，以欺骗防御者不去攻这个套。
防御时计算赢墩
一个好的防御者，必须在牌局的整个过程中，随时计算对方的赢墩，并试图去算出他手中的牌。假如防御者能进行这种计算，并保持清醒头脑，有些定约就不难击垮。经常有这样的情况，即如果定约者持有某一张牌时就能完成定约，则防御者想击败定约的唯一希望就是假设他没有这张牌。防御者不算定约者的赢墩就会垫错牌，对此，S.J.Simon举出一个例子：
定约是3NT。西首攻J，定约者放过二轮，第三轮拿进，然后飞一张草花，东家拿进，出掉第十三张红心，打出一张草花。南家这时已丢四墩，如果西家保持警觉，他应看到，定约者稳拿八墩——四墩草花、两墩方块、一墩红心、一墩黑桃。当草花打完之后，十个桥手中有九个坐在西家位置时要垫方块，因为方块不能拿墩，而Q可能拿墩。其实，既然定约者能稳拿8墩，西家必须假设他的同伴有K才能击败定约。因此，他应该垫掉黑桃而保留方块，这样南家就无从决定究竟该飞哪一家的Q了。
有经验的防御者，常常采取提前考虑的策略，即在一张无关紧要的牌打出来时，停下来考虑他们的防御路线。所以上述例子中西家不应该在出第四轮或第五轮草花时才考虑如何垫牌，而应在第三轮时就提前考虑。防御者只有提前考虑好防御路线，才能在牌局接近终局变得真正困难时，不至于在垫牌上发生问题，从而使定约者打起牌来更为困难些。防御者如估计到以后垫牌会发生困难，他可以偷偷地先垫掉大牌的保护张，这并不会冒太大风险的。
注意牌局的进行情况
本章的整个课题是要不断地估算各家的牌型和赢墩来源，这种努力所收的效果比起通晓各种桥牌知识和能打出各种精采妙招来都要大得多。下面这手牌并没有什么难处，但仍然使一个好的桥手在防御中三此发生错误，之所以如此，就是因为他没有去考虑定约者如何才能拿足十墩牌。
南家曾叫过红心和方块，定约是4。西家出K，东家出6，这是一个错误的信号，因为东家没有任何理由去鼓励西家继续出黑桃，然而，西家不理这个信号，正确地出了张将牌，定约者拿进，打出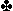10，西家出5，东家用Q拿进。这时东家有好几条防御路线，最为安全的打法是立即出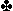A再出一张草花。西家出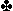5已表示他只有两张草花，所以东家知道，南家必须将吃第三轮草花。南家可能吊完将牌，然后兑现明手的草花长套。但是，这样他就只能拿到五墩将牌、三墩草花和一墩方块。另一个防御方法是出K，这样当东家再用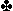A进手后就可打出Q而逼明手将吃，从而可以防止草花的树立。然而，在实战中，东家出了张将牌，这或许是最明显的合理打法，但当然不是最好的打法。这时定约者手中的大牌拿进，出第二张草花，东家用A拿进，剩下的牌是：
这时东家出一张草花是完全必要的，然而他却出了张Q，他以为唯一能击败定约的希望是南家有第二张黑桃，东家只有仔细地计算定约者的赢墩才能确定最好的防御方法。如果东家在第一次拿到出牌权时，就出K，就可以使对方宕两墩，因为可算出南家只能拿到五墩将牌，两墩将吃和一墩A。
