|
专家打法
Terence
Reese
著
|
 返回目录 返回目录
|
第三章
限制性选择的原理
早在1950年,托拉斯柯特(Alan
Truscott)就曾经在一本杂志上发表了一篇有关打牌原理的文章,当时所产生的效果只是被人模模糊糊地理解了一些,一般说来,当时还是没有归纳出一套完整的理论。
请比较下面这两种情形:
|
(1)
|
A1073
|
(2)
|
A973
|
|
|

|
|

|
|
|
KQ5
|
|
KQ5
|
在第一个例中,庄家先打掉K—Q,再打5;前面两圈敌方两家都垫小牌,现在南家必须决定要用10偷,还是用A硬敲。现在唯一的线索是东家比西家还多了一张未知的牌,由或然率来看,硬敲J的机会比较大。(虽然4—2分配的可能性比3—3分配大,但是4—2分配中包括了J—×两张,而这种可能性已经不存在了。)
在第二个例子,庄家先打K—Q,东家落下10—×;他继续打5,西放小,庄家又遇到了同样的选择,偷吃?还是硬敲呢?在这里偷到机会是否仍和例(1)相似呢?
如果有人告诉你这时候有利于偷牌的比例是2:1,你也许会感到非常惊奇;但是不管对于这种情况有多少种不同的解释,其中最简单的一种就是:假如东家握着J—10—×,那么他第二圈大半会下J。
同样的理由也可以应用在许多桥手们所熟知的情况上。例如:
|
AQJ973
|
|

|
|
10842
|
南家先引10,西家下5,现在只缺两张牌,6和K;有人说:“东家持有单张K和持有单张6的机会均等,所以我会下A。”
大部分的桥手都知道,即使不考虑3—0分配的情况,对于不平均分配还是用硬敲比较好。认为东家有单张K和单张6的机会相同是不正确的;假如西家持6—5双张,那么在第一圈他可以下6;如果西家是持有K—5,那么他的选择就被限制了,他必须下5。
下面是另一种非常普通的情况,大多数的桥手都可以由直觉或经验中得到正确的打法:
|
AJ1075
|
|

|
|
9842
|
南家引9,东家以K或Q吃进。庄家下一圈当然再偷一次,因为东家可以从K—Q中毫无区别的随便打出一张牌来,所以不论他打那一张,我们都可以得到一个指示,就是他没有另一张。
下面还有一种情形,桥手们都会自觉地或不觉地被限制选择的原理所指引:
|
K10953
|
|

|
|
72
|
在用9偷而被东家Q或J吃进之后,第二圈还是应该用10偷;还有两张大牌在外头,为什么不下K呢?答案还是一样的:东家打出Q或J中的一张,就等于对我们提供了他没有另外一张的推测。
较优的推测
上面最后谈到的这个问题的根据讨论起来相当复杂,我们只能藉前面所举的例子来印证一下。在最后一个例子中,东家持有A—J—×或A—Q—×的机会超过他持有Q—J—×的机会;同样地前面例(2)中,东家持有J—×或10—×的可能性明显地超过持有J—10—×的可能性。
一些出乎意料的结论
了解了我们前面所讨论的原则之后,你将可以解决许多本来在牌桌上很难取舍的问题。
|
A108642
|
|

|
|
K95
|
打K的时候东家掉下了Q,现在南家应该打东家是Q—J双张呢?还是单张Q呢?答案是:偷的机会似乎是硬敲的两倍。再度(如果理由是正确的话,那么应该永远是如此的)使用较优的推测,我们可以发现东家是单张Q或J的机会比他拥有Q—J的机会为大。
当庄家上下手之间少了一张牌的时候,就不是那么容易可以用或然率来推测了:
|
A10864
|
|

|
|
K95
|
同样的,在第一圈打出K的时候,东家还是掉下一张大牌。现在,除了东家掉下的J(或者Q)提供了他没有另一张大牌的推测,庄家还必须考虑外家五张牌3—2分配的机会:Q—J只是十种双张组合中的一种,单张Q和单张J占五种单张分配中的两种;所以虽然东家是双张的机会比单张的机会大,但是Q—J双张的可能性仍然很微小。
请注意下面这两种情况所产生的差异:
|
(1)
|
AQ864
|
(2)
|
AQ964
|
|
|

|
|

|
|
|
J753
|
|
J753
|
在(1)中,南家引J,西家下K,明家A吃,东家掉下9或10。按照我们所复习的原理,在下一圈用8偷牌对于不平均分配是比较有利的,同时东家掉下9也提供了他没有10的推测。
在(2)中,南家引J,西家下K,明家A吃,东家掉下8。现在庄家要偷还是要硬敲是一个问题;东家掉下8,对于10并没有透露任何消息。假如他是从10—8中掉下8,那么他的垫牌是受到限制的;如果他是从10—9垫牌,那么他就可以随意垫了。
下面这个例子极富启发性:
|
Q97642
|
|

|
|
A5
|
南家引A打落了东家的10或J。庄家第二圈就要考虑到底是用9偷还是下Q;如果他们跟了Q而却被K吃进,他们就会说:“东家持有J—10的机会和他持有K—10的机会一样。”但是我们已经看过了,这种想法是不对的:如果东家持有J—10双张,那么他可以随便垫一张牌,但是如果他持有K—10或K—J的话,他就没有选择的余地了。
这里又是一个很普通的情况:
|
Q742
|
|

|
|
K9653
|
南家引3,西家下10,明家的Q被东家A吃住。不需要再重复一遍理由,我们都知道在拉还手上的时候,庄家必须用9偷。
在这种情况下,庄家必须假定防家是一无选择的余地,而不假定防家是运用特殊的方法去选择。在1955年世界冠军赛中,有一副美国队做庄的牌,庄家如果得到了正确的推论,他就可以挽救危机了:
|
|
 10 10
|
|
|
 A7 A7
|
|
 AK932 AK932
|
|
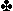 KJ974 KJ974
|
|
 QJ53 QJ53
|

|
 A9762 A9762
|
|
 105 105
|
 QJ94 QJ94
|
|
 J5 J5
|
 Q107 Q107
|
|
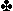 108532 108532
|
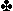 Q Q
|
|
|
 K84 K84
|
|
|
 K8632 K8632
|
|
 864 864
|
|
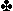 A6 A6
|
史比罗(Schapiro)和我在首引黑桃且续引黑桃的情况下完成了4 ,在另一桌美国南家主打3NT。首引黑桃,东家吃进,回攻黑桃。这时候庄家似乎可以取得九墩牌了——一墩黑桃、两墩红心、两墩方块和四墩梅花,但是实际上合约却垮了一墩,原因是庄家在第二圈打梅花的时候并没有用
,在另一桌美国南家主打3NT。首引黑桃,东家吃进,回攻黑桃。这时候庄家似乎可以取得九墩牌了——一墩黑桃、两墩红心、两墩方块和四墩梅花,但是实际上合约却垮了一墩,原因是庄家在第二圈打梅花的时候并没有用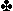 9偷,他猜想东家的Q是从Q—10中引出的假牌,这种想法当然也有可能,但是观察这个问题的方法是:假如东家持有Q—10,他可能会下10;但是如果是单张Q,那么他只能下Q了;因此即使4—2分配的可能性较大,还是可以猜出东家是单张Q。
9偷,他猜想东家的Q是从Q—10中引出的假牌,这种想法当然也有可能,但是观察这个问题的方法是:假如东家持有Q—10,他可能会下10;但是如果是单张Q,那么他只能下Q了;因此即使4—2分配的可能性较大,还是可以猜出东家是单张Q。
掷币实验
许多读者可能会认为本章的那一些结论很难以接受。一个深信分配的情形随着每副牌改变的桥手,他将不容易了解回过头来研究较优可能性的好处。为了消除这种错觉,我们将利用其他的东西代替桥牌来做些实验。
假设有五个铜板,四个正面,一个反面,分成两堆,三个在左边,两个在右边;你会说,3:2,不利于反面在少的那一堆。现在从多的那一堆拿去两个,条件是两个都不能是反面(换到桥牌上来讲,这就是所垫的牌是可选择的和持有大牌K或Q不能任意垫的情形),现在只有一个铜板在左边,而仍有两个铜板在右边,但却仍是3:2,不利于反面在右边。
